Segmentation Faults Can Sometimes Be Fixed by Performing What Two Tasks Below?ã¢â‚¬â€¹

Do y'all really understand Big O? If and so, and so this will refresh your understanding earlier an interview. If not, don't worry — come and bring together the states for some endeavors in computer scientific discipline.
If you take taken some algorithm related courses, you've probably heard of the term Big O notation. If you haven't, we will go over it here, and and so get a deeper understanding of what information technology really is.
Big O notation is 1 of the most fundamental tools for computer scientists to analyze the cost of an algorithm. It is a adept practice for software engineers to understand in-depth as well.
This article is written with the assumption that yous accept already tackled some code. Also, some in-depth textile also requires high-school math fundamentals, and therefore can be a bit less comfortable to total beginners. But if you are set, let'south get started!
In this article, we volition have an in-depth word about Large O notation. Nosotros volition showtime with an example algorithm to open up our understanding. Then, nosotros volition go into the mathematics a lilliputian bit to have a formal understanding. After that we will go over some common variations of Big O notation. In the end, we volition discuss some of the limitations of Large O in a applied scenario. A tabular array of contents can be found beneath.
Table of Contents
- What is Big O notation, and why does it matter
- Formal Definition of Big O notation
- Large O, Little O, Omega & Theta
- Complexity Comparison Between Typical Big Bone
- Time & Space Complexity
- Best, Average, Worst, Expected Complexity
- Why Big O doesn't matter
- In the end…
So let's get started.
1. What is Big O Annotation, and why does information technology matter
"Big O note is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. It is a member of a family unit of notations invented by Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau annotation or asymptotic notation."— Wikipedia'southward definition of Big O notation
In manifestly words, Big O notation describes the complexity of your code using algebraic terms.
To understand what Big O annotation is, we tin can accept a look at a typical example, O(n²) , which is usually pronounced "Large O squared" . The letter "north" here represents the input size, and the office "one thousand(n) = due north²" within the "O()" gives us an thought of how circuitous the algorithm is with respect to the input size.
A typical algorithm that has the complication of O(northward²) would exist the selection sort algorithm. Selection sort is a sorting algorithm that iterates through the list to ensure every element at index i is the ith smallest/largest element of the listing. The CODEPEN below gives a visual case of it.
The algorithm tin be described by the post-obit code. In social club to brand sure the ith element is the ith smallest chemical element in the list, this algorithm offset iterates through the list with a for loop. And so for every element it uses some other for loop to find the smallest chemical element in the remaining function of the list.
SelectionSort(List) { for(i from 0 to Listing.Length) { SmallestElement = List[i] for(j from i to Listing.Length) { if(SmallestElement > List[j]) { SmallestElement = List[j] } } Bandy(Listing[i], SmallestElement) } } In this scenario, we consider the variable List as the input, thus input size n is the number of elements inside Listing . Assume the if statement, and the value assignment bounded by the if argument, takes constant time. Then we can detect the big O note for the SelectionSort office by analyzing how many times the statements are executed.
First the inner for loop runs the statements within north times. And then afterward i is incremented, the inner for loop runs for due north-1 times… …until it runs in one case, so both of the for loops reach their terminating conditions.
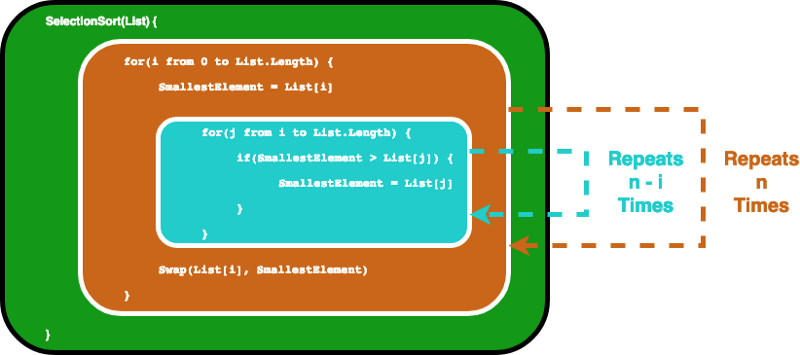
This actually ends up giving us a geometric sum, and with some high-school math we would detect that the inner loop will echo for 1+2 … + n times, which equals due north(north-one)/2 times. If we multiply this out, we volition end upwards getting n²/2-northward/2.
When we calculate large O notation, we only care near the ascendant terms, and we practise not care about the coefficients. Thus we take the northward² as our terminal big O. We write it as O(northward²), which again is pronounced "Big O squared".
Now y'all may be wondering, what is this "dominant term" all well-nigh? And why practice we non care about the coefficients? Don't worry, we will go over them one by 1. Information technology may exist a little bit hard to understand at the beginning, just it will all make a lot more sense every bit you read through the adjacent department.
2. Formal Definition of Big O notation
Once upon a time there was an Indian king who wanted to reward a wise homo for his excellence. The wise man asked for cipher but some wheat that would fill upward a chess lath.
But here were his rules: in the commencement tile he wants 1 grain of wheat, and so 2 on the second tile, then iv on the adjacent one…each tile on the chess lath needed to exist filled past double the amount of grains as the previous i. The naïve king agreed without hesitation, thinking information technology would be a little demand to fulfill, until he actually went on and tried it…

And so how many grains of wheat does the king owe the wise man? Nosotros know that a chess board has eight squares by eight squares, which totals 64 tiles, so the final tile should take 2⁶⁴ grains of wheat. If you practice a adding online, you will finish up getting i.8446744*x¹⁹, that is about xviii followed past xviii zeroes. Assuming that each grain of wheat weights 0.01 grams, that gives us 184,467,440,737 tons of wheat. And 184 billion tons is quite a lot, isn't it?
The numbers grow quite fast after for exponential growth don't they? The same logic goes for computer algorithms. If the required efforts to accomplish a task abound exponentially with respect to the input size, it tin end up becoming enormously large.
At present the square of 64 is 4096. If you add that number to two⁶⁴, information technology volition exist lost outside the significant digits. This is why, when we look at the growth rate, we but intendance nigh the dominant terms. And since we want to analyze the growth with respect to the input size, the coefficients which just multiply the number rather than growing with the input size do not comprise useful information.
Below is the formal definition of Big O:

The formal definition is useful when yous need to perform a math proof. For case, the time complication for option sort tin be defined by the office f(north) = north²/2-n/two equally we have discussed in the previous section.
If we allow our function k(due north) to be northward², we tin find a constant c = i, and a Due north₀ = 0, and and then long equally North > N₀, N² will always exist greater than Due north²/2-N/two. We tin easily testify this by subtracting N²/2 from both functions, so nosotros tin easily see N²/2 > -N/2 to be true when N > 0. Therefore, we can come upward with the decision that f(n) = O(n²), in the other pick sort is "big O squared".
You might take noticed a piffling trick here. That is, if you make k(northward) grow supper fast, manner faster than anything, O(g(n)) will always be dandy enough. For case, for any polynomial function, you can always be right by proverb that they are O(2ⁿ) considering 2ⁿ will eventually outgrow any polynomials.
Mathematically, you are correct, simply mostly when nosotros talk nearly Big O, we desire to know the tight leap of the function. You lot volition understand this more than as you lot read through the next section.
Just before we go, let's exam your understanding with the following question. The answer volition be constitute in later sections so it won't be a throw abroad.
Question: An image is represented past a 2d array of pixels. If you use a nested for loop to iterate through every pixel (that is, you have a for loop going through all the columns, then another for loop within to go through all the rows), what is the time complexity of the algorithm when the image is considered every bit the input?
3. Big O, Little O, Omega & Theta
Large O: "f(n) is O(g(due north))" iff for some constants c and North₀, f(North) ≤ cg(Northward) for all N > N₀Omega: "f(n) is Ω(thou(northward))" iff for some constants c and N₀, f(North) ≥ cg(Northward) for all N > N₀
Theta: "f(n) is Θ(g(due north))" iff f(n) is O(m(n)) and f(n) is Ω(m(northward))
Little O: "f(north) is o(grand(due north))" iff f(northward) is O(yard(northward)) and f(n) is non Θ(grand(due north))
—Formal Definition of Big O, Omega, Theta and Little O
In evidently words:
- Big O (O()) describes the upper bound of the complexity.
- Omega (Ω()) describes the lower bound of the complication.
- Theta (Θ()) describes the verbal bound of the complication.
- Little O (o()) describes the upper bound excluding the exact leap.
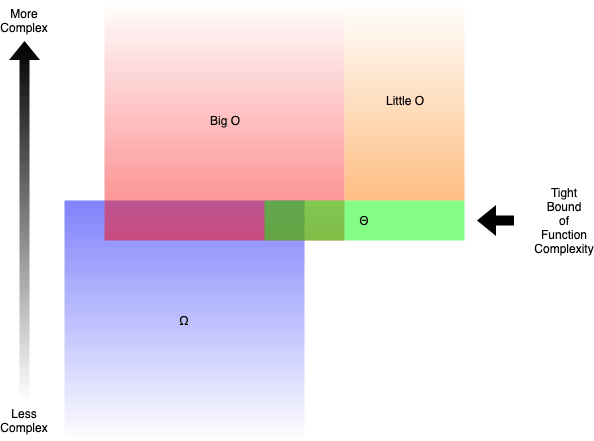
For example, the function g(n) = n² + 3n is O(n³), o(n⁴), Θ(north²) and Ω(due north). But you would still exist right if you say it is Ω(northward²) or O(n²).
Generally, when nosotros talk nigh Big O, what we actually meant is Theta. It is kind of meaningless when you lot give an upper bound that is fashion larger than the scope of the analysis. This would be similar to solving inequalities by putting ∞ on the larger side, which will almost always brand you lot right.
Only how exercise we decide which functions are more complex than others? In the next section y'all volition be reading, we will learn that in item.
4. Complexity Comparing Between Typical Big Bone
When we are trying to figure out the Large O for a particular part m(due north), we only care almost the ascendant term of the function. The dominant term is the term that grows the fastest.
For example, n² grows faster than north, so if we have something like k(north) = n² + 5n + 6, it will be big O(n²). If you accept taken some calculus earlier, this is very similar to the shortcut of finding limits for partial polynomials, where you simply intendance well-nigh the dominant term for numerators and denominators in the end.

But which function grows faster than the others? There are actually quite a few rules.
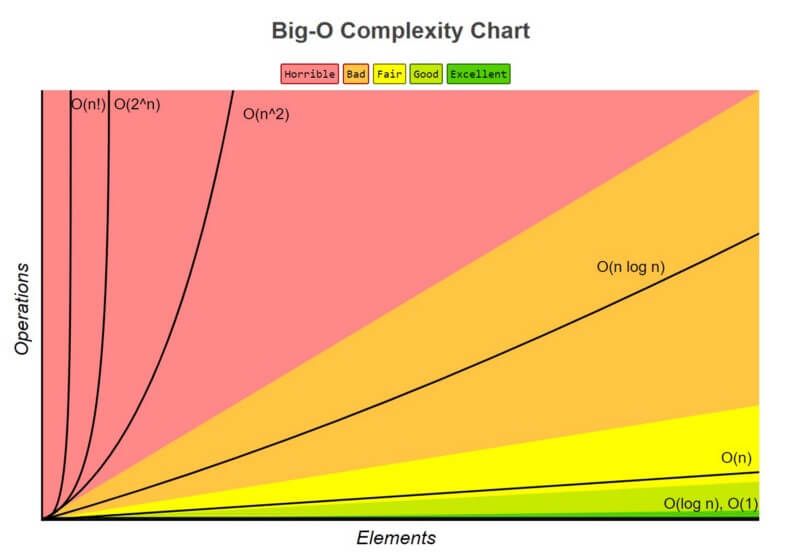
1. O(1) has the least complexity
Ofttimes called "constant fourth dimension" , if you can create an algorithm to solve the trouble in O(1), you are probably at your all-time. In some scenarios, the complexity may go beyond O(1), and so we can clarify them by finding its O(one/yard(n)) counterpart. For example, O(ane/n) is more complex than O(one/n²).
2. O(log(n)) is more complex than O(i), simply less complex than polynomials
Every bit complication is often related to split and conquer algorithms, O(log(n)) is generally a good complexity you lot tin can reach for sorting algorithms. O(log(n)) is less circuitous than O(√due north), considering the foursquare root function tin exist considered a polynomial, where the exponent is 0.five.
3. Complexity of polynomials increases as the exponent increases
For case, O(n⁵) is more complex than O(n⁴). Due to the simplicity of it, we really went over quite many examples of polynomials in the previous sections.
4. Exponentials accept greater complexity than polynomials as long as the coefficients are positive multiples of n
O(2ⁿ) is more circuitous than O(due north⁹⁹), simply O(2ⁿ) is actually less complex than O(1). We more often than not take ii as base for exponentials and logarithms because things tends to be binary in Informatics, but exponents tin can be changed past changing the coefficients. If not specified, the base for logarithms is causeless to be 2.
5. Factorials have greater complexity than exponentials
If you are interested in the reasoning, look upwards the Gamma function, it is an analytic continuation of a factorial. A short proof is that both factorials and exponentials accept the same number of multiplications, but the numbers that become multiplied grow for factorials, while remaining constant for exponentials.
6. Multiplying terms
When multiplying, the complication volition be greater than the original, simply no more than the equivalence of multiplying something that is more than complex. For example, O(n * log(n)) is more complex than O(n) only less complex than O(due north²), because O(n²) = O(northward * n) and n is more than circuitous than log(n).
To examination your understanding, endeavor ranking the post-obit functions from the nigh complex to the charter complex. The solutions with detailed explanations can be found in a later department every bit you read. Some of them are meant to be tricky and may require some deeper understanding of math. As you get to the solution, you volition sympathise them more.
Question: Rank post-obit functions from the virtually complex to the charter circuitous.
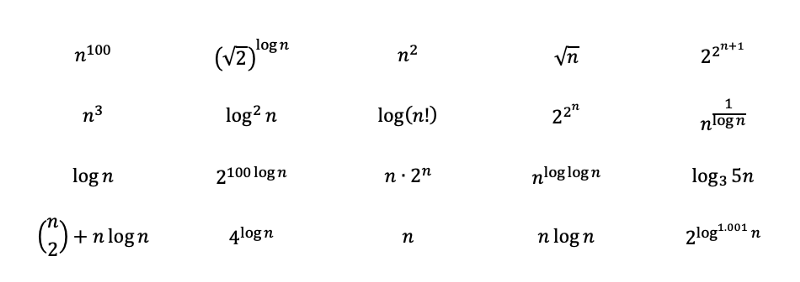
Solution to Section ii Question:It was actually meant to be a play a joke on question to test your understanding. The question tries to brand you reply O(due north²) because there is a nested for loop. However, n is supposed to be the input size. Since the epitome array is the input, and every pixel was iterated through only in one case, the answer is really O(n). The side by side department volition get over more examples similar this i.
5. Time & Space Complexity
And so far, nosotros have only been discussing the time complexity of the algorithms. That is, nosotros only care about how much fourth dimension information technology takes for the programme to consummate the chore. What also matters is the space the program takes to complete the chore. The space complexity is related to how much memory the program will use, and therefore is besides an of import factor to analyze.
The space complexity works similarly to fourth dimension complication. For example, option sort has a space complication of O(1), because it only stores ane minimum value and its index for comparing, the maximum infinite used does not increment with the input size.
Some algorithms, such every bit bucket sort, take a infinite complexity of O(n), but are able to chop down the fourth dimension complexity to O(1). Saucepan sort sorts the array by creating a sorted list of all the possible elements in the array, then increments the count whenever the chemical element is encountered. In the end the sorted array will be the sorted list elements repeated by their counts.
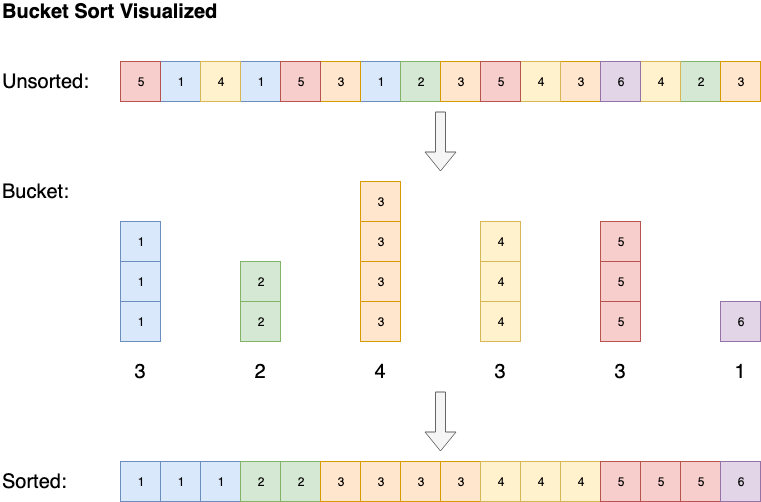
vi. All-time, Boilerplate, Worst, Expected Complexity
The complication can also be analyzed equally best example, worst case, average instance and expected instance.
Let'south accept insertion sort, for example. Insertion sort iterates through all the elements in the list. If the chemical element is larger than its previous element, it inserts the chemical element backwards until it is larger than the previous element.
If the assortment is initially sorted, no swap will exist made. The algorithm will only iterate through the assortment one time, which results a fourth dimension complexity of O(n). Therefore, we would say that the best-case time complication of insertion sort is O(n). A complexity of O(n) is as well frequently called linear complication.
Sometimes an algorithm just has bad luck. Quick sort, for instance, will have to go through the listing in O(n) time if the elements are sorted in the opposite club, only on average information technology sorts the assortment in O(n * log(n)) fourth dimension. Generally, when we evaluate time complexity of an algorithm, we look at their worst-case performance. More than on that and quick sort will be discussed in the side by side section as you read.
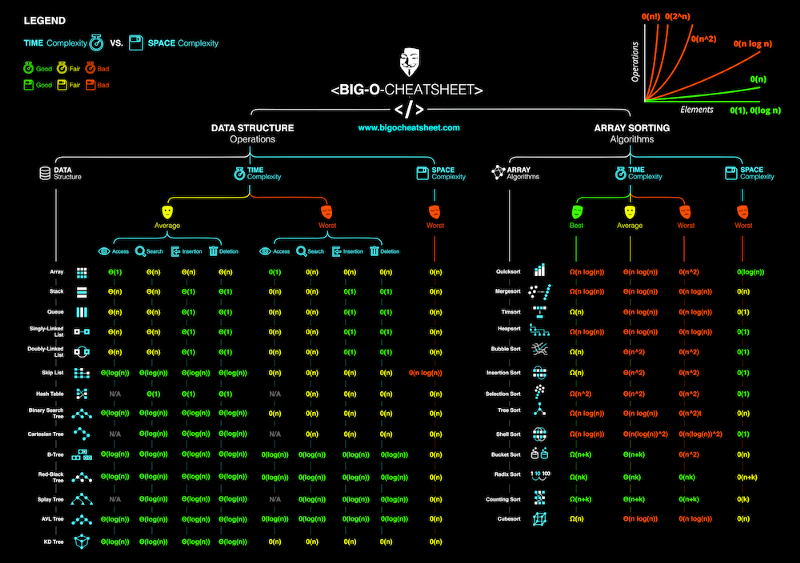
The boilerplate case complication describes the expected performance of the algorithm. Sometimes involves calculating the probability of each scenarios. Information technology tin can get complicated to become into the details and therefore non discussed in this commodity. Below is a cheat-sheet on the time and space complexity of typical algorithms.
Solution to Section 4 Question:
By inspecting the functions, we should be able to immediately rank the following polynomials from nigh circuitous to lease complex with dominion three. Where the square root of n is just n to the ability of 0.5.
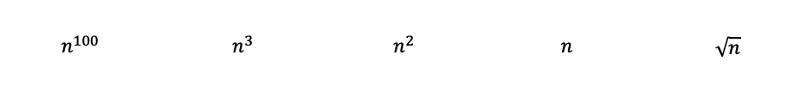
Then by applying rules 2 and 6, we will go the post-obit. Base 3 log can be converted to base 2 with log base of operations conversions. Base of operations three log still grows a little bit slower so base of operations 2 logs, and therefore gets ranked after.
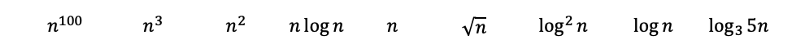
The rest may wait a little bit tricky, but let'south endeavour to unveil their truthful faces and run into where nosotros tin can put them.
First of all, 2 to the ability of 2 to the power of n is greater than 2 to the power of n, and the +1 spices it up even more than.

And and so since nosotros know two to the ability of log(n) with based ii is equal to northward, we tin convert the following. The log with 0.001 as exponent grows a piffling chip more than than constants, but less than almost anything else.

The i with n to the power of log(log(due north)) is actually a variation of the quasi-polynomial, which is greater than polynomial but less than exponential. Since log(north) grows slower than northward, the complication of it is a bit less. The 1 with the inverse log converges to constant, every bit 1/log(n) diverges to infinity.

The factorials can exist represented by multiplications, and thus can be converted to additions outside the logarithmic function. The "n choose 2" tin be converted into a polynomial with a cubic term being the largest.

And finally, we tin rank the functions from the most complex to the least complex.
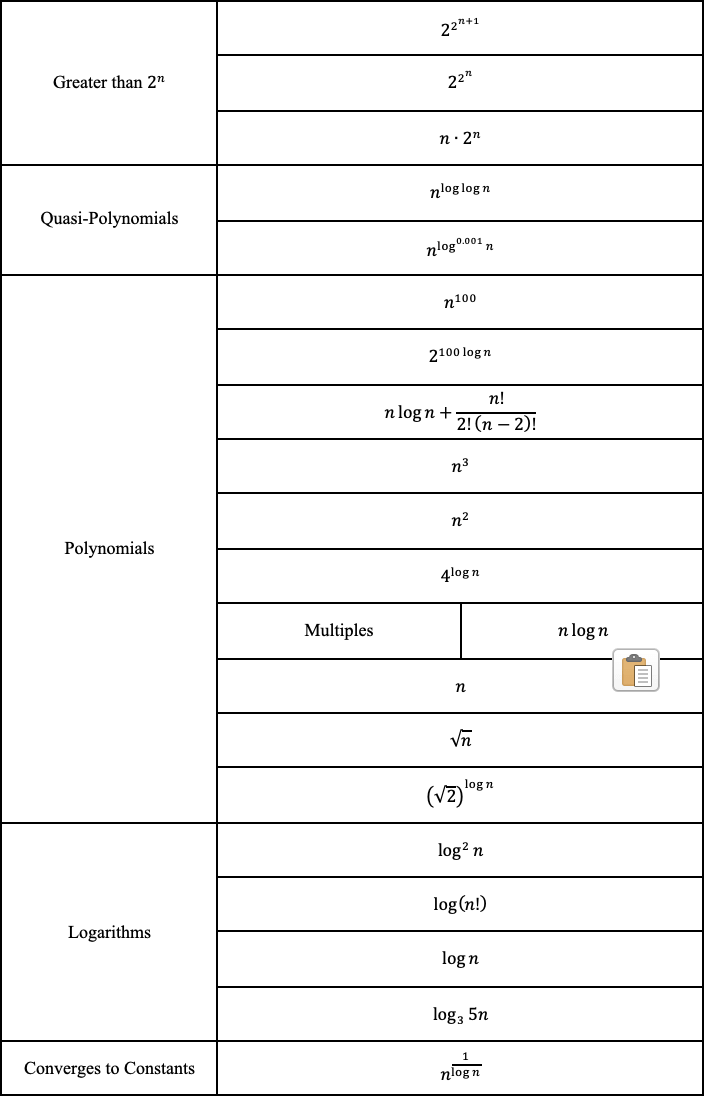
Why BigO doesn't matter
!!! — WARNING — !!!Contents discussed hither are generally not accustomed by most programmers in the earth. Discuss information technology at your own risk in an interview. People really blogged about how they failed their Google interviews because they questioned the authorization, like here.
!!! — Alarm — !!!
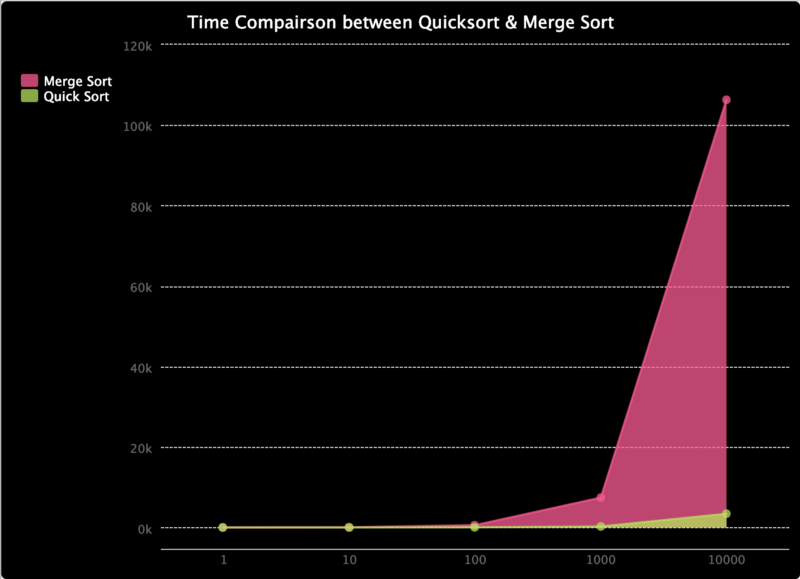
Since we take previously learned that the worst case time complexity for quick sort is O(northward²), only O(n * log(n)) for merge sort, merge sort should be faster — right? Well you probably have guessed that the answer is faux. The algorithms are just wired upwards in a way that makes quick sort the "quick sort".
To demonstrate, cheque out this trinket.io I fabricated. It compares the time for quick sort and merge sort. I accept merely managed to examination it on arrays with a length up to 10000, but as you lot can come across so far, the fourth dimension for merge sort grows faster than quick sort. Despite quick sort having a worse case complication of O(n²), the likelihood of that is really low. When it comes to the increment in speed quick sort has over merge sort bounded by the O(n * log(n)) complexity, quick sort ends up with a meliorate performance in average.
I take as well made the below graph to compare the ratio between the time they accept, as it is difficult to see them at lower values. And as yous can come across, the percentage fourth dimension taken for quick sort is in a descending order.
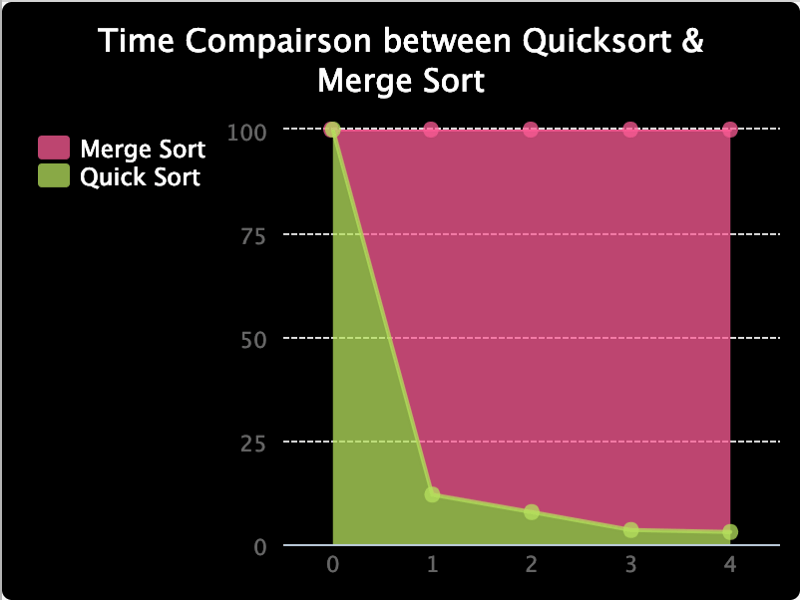
The moral of the story is, Big O annotation is only a mathematical analysis to provide a reference on the resources consumed by the algorithm. Practically, the results may be dissimilar. But it is more often than not a practiced practice trying to chop downwardly the complexity of our algorithms, until nosotros run into a case where we know what nosotros are doing.
In the end…
I like coding, learning new things and sharing them with the community. If in that location is anything in which you are specially interested, delight let me know. I generally write on web design, software architecture, mathematics and information scientific discipline. Yous tin detect some dandy articles I have written before if you are interested in any of the topics above.
Promise you take a great time learning informatics!!!
Learn to code for costless. freeCodeCamp'due south open source curriculum has helped more than forty,000 people go jobs as developers. Get started
napoleonbuffive94.blogspot.com
Source: https://www.freecodecamp.org/news/big-o-notation-why-it-matters-and-why-it-doesnt-1674cfa8a23c/
0 Response to "Segmentation Faults Can Sometimes Be Fixed by Performing What Two Tasks Below?ã¢â‚¬â€¹"
Postar um comentário